CARBONE TETRAEDRIQUE


RETOUR AU SOMMAIRE


Dans le méthane, l' angle entre deux liaisons C-H est 109°28'.
La géométrie de la molécule est la suivante : Le carbone occupe le centre d'un tétraèdre régulier aux sommets duquel se placent les quatre atomes d'hydrogène.
Le but de ce travail est de démontrer que les angles ainsi définis valent bien 109°28'.

O est le centre du tétraèdre.Nous donnerons aux côtés du tétraèdre la valeur 1 (AB = AC = AD = BC =BD =CD =1)
L'angle BOC dont nous recherchons la valeur correspond à 2a (a représentant l'angle BOH').
Montrons que dans ces conditions :
    - 
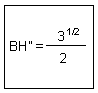
Triangle BH"C rectangle en H":
(BH")2 + (H"C)2 = (BC)2
H"C = 1/2    et BC = 1
(BH")2 = 12 - (1/2)2 = 3/4
BH" =(3)1/2 /2

    - 
Propriété de H :
BH = 2/3 BH"
BH = 2/3 x (3)1/2 /2
BH = 1/(3)1/2

    - 
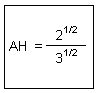
Triangle AHB rectangle en H :
(AH)2 +(BH)2 = (AB)2
(AH)2 = 12 - (1/(3)1/2)2 = 1 - 1/3 = 2/3
AH = (2)1/2/(3)1/2

    - 
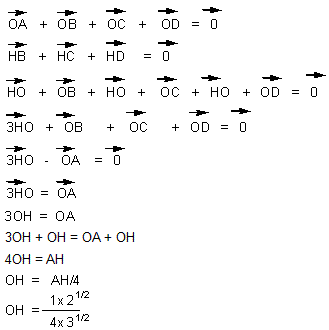
TETRAEDRIQUE1.gif

    - 
Triangle OHB rectangle en H :
(OB)2 = (OH)2 + (BH)2
(OB)2 = 2/ (42x3)  +  1/3 = (1/3) ( 1/23 + 1)

(OB)2 = (1/3) (1/8 + 1) = (1/3) (9/8) = 3/8

(OB)2 = 3/(2x22) = (1/22) (3/2)
OB = (1/2) x (3/2)1/2

 

On peut alors calculer dans le triangle OH'B rectangle en H' :
sin(a) = BH'/OB en remarquant que BH' = 1/2
sin(a) =(1/2)/((1/2)x(3/2)1/2) = (2/3)1/2
a = Arcsin((2/3)1/2)
Soit
2a =2 Arcsin((2/3)1/2) = 109,47122°
2a =109° 28' 16,394268"