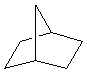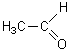---

LE DEGRE D'INSATURATION DES MOLECULES

---

RETOUR AU SOMMAIRE

---

1) Définition:
C'est la somme du nombre de liaisons p et du nombre de cycles d'une molécule.

Exemples:

Formule brute	Formule topologique	Nom	Degré d'insaturation
C5H12		Pentane	Degré d'insaturation (DI) = 0  Pas de liaison p Pas de cycle.
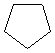
C5H10		Cyclopentane	DI = 1 Un cycle
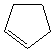
C5H8		Cyclopentène	DI = 2 Une liaison p Un cycle
C6H12		2-méthylpent-1-ène	DI = 1 Une liaison p
C7H12		Norbornane	DI = 2 Deux cycles
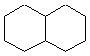
C10H18		Décaline	DI = 2 Deux cycles
C2H6O		Méthoxyméthane	DI = 0 Pas de liaison p Pas de cycle.
C2H4O		Ethanal	DI = 1 Une liaison p
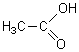
C2H4O2		Acide éthanoïque	DI = 1 Une liaison p
CH5N		Méthanamine	DI = 0 Pas de liaison p Pas de cycle.
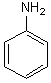
C6H7N		Aniline	DI = 4 Trois "liaisons p " Un cycle.
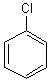
C6H5Cl		Chlorobenzène	DI = 4 Trois "liaisons p " Un cycle.

2) Intérêt de ce paramètre:
Déterminer le degré d'insaturation d'une molécule à partir de sa formule semi-développée, développée ou topologique, ne présente pas beaucoup d'intérêt. Par contre le déterminer à partir de sa formule moléculaire permet d'obtenir un indice qui, associé à d'autres provenant des différentes méthodes spectroscopiques (IR, RMN, Spectre de masse...) conduit à la détermination de la structure de la molécule et donc à sa formule développée.

3) Détermination du degré d'insaturation à partir de la formule brute:
C'est la comparaison entre le nombre d'hydrogènes qui existent dans la molécule H_effectif et le nombre d'hydrogènes qui existeraient dans l'hydrocarbure saturé ayant le même nombre de carbones H_sat qui permet d'obtenir le degré d'insaturation:

 DI =(H_sat-H_effectif)/2

    3-1) Exemples à partir d'hydrocarbures:
        a) C₅H₁₂  H_effectif=12 H_sat :n_C=5    n_H=2n_C+2 =12    H_sat=n_H=12        DI =(H_sat-H_effectif)/2=(12-12)/2  =  0 C'est le cas du pentane.
        b) C₅H₁₀  H_effectif=10 H_sat :n_C=5    n_H=2n_C+2 =12    H_sat=n_H=12        DI =(H_sat-H_effectif)/2=(12-10)/2  =  1 C'est le cas du cyclopentane.
        c) C₅H₈    H_effectif=8 H_sat :n_C=5    n_H=2n_C+2 =12    H_sat=n_H=12        DI =(H_sat-H_effectif)/2=(12-8)/2  =  2 C'est le cas du cyclopentène.
        d) C₆H₁₂  H_effectif=12 H_sat :n_C=6   n_H=2n_C+2 =14    H_sat=n_H=14        DI =(H_sat-H_effectif)/2=(14-12)/2  =  1 C'est le cas du 2-méthylpent-1-ène.
        e) C₇H₁₂  H_effectif=12 H_sat :n_C=7   n_H=2n_C+2 =16   H_sat=n_H=16        DI =(H_sat-H_effectif)/2=(16-12)/2  =  2 C'est le cas du Norbornane.
        f) C₁₀H₁₈  H_effectif=18 H_sat :n_C=10   n_H=2n_C+2 =22    H_sat=n_H=22        DI =(H_sat-H_effectif)/2=(22-18)/2  =  2 C'est le cas de la décaline.

    3-2) Exemples à partir de composés oxygénés (ou soufrés):
La façon de déterminer le degré d'insaturation est le même que pour les hydrocarbures:
        g) C₂H₆O H_effectif=6 H_sat :n_C=2   n_H=2n_C+2 =6    H_sat=n_H=6        DI =(H_sat-H_effectif)/2=(6-6)/2  =  0 C'est le cas du méthoxyméthane.
        h) C₂H₄O H_effectif=4 H_sat :n_C=2   n_H=2n_C+2 =6    H_sat=n_H=6        DI =(H_sat-H_effectif)/2=(6-4)/2  =  1 C'est le cas de l'éthanal.
        i) C₂H₄O₂ H_effectif=4 H_sat :n_C=2   n_H=2n_C+2 =6    H_sat=n_H=6        DI =(H_sat-H_effectif)/2=(6-4)/2  =  1 C'est le cas de l'acide éthanoïque.

    3-3) Exemples à partir de composés azotés:
Si l' on applique à la méthanamine (CH₃-NH₂), la règle appliquée aux hydrocarbures ou aux composés oxygénés, on trouve: H_sat=4 et H_effectif=5 soit DI =(H_sat-H_effectif)/2=(4-5)/2 = -0,5 ce qui n'a aucun sens (le vrai DI est 0 nous l'avons vu). De même pour l'aniline (C₆H₇N), on trouve: H_sat=14 et H_effectif=7 soit DI =(H_sat-H_effectif)/2=(14-7)/2 = 3,5 le vrai DI étant égal à 4.
Il faut donc pour les composés azotés utiliser une autre règle pour le calcul de H_sat :

H_sat = 2n_C+2+n_N

et procéder comme avec les autres composés:
Ainsi pour la méthanamine: H_sat=2x1+2+1=5   H_effectif=5 soit DI =(H_sat-H_effectif)/2=(5-5)/2 = 0 On retrouve la bonne valeur. Et pour l'aniline: H_sat=2x6+2+1=15    H_effectif=7 soit DI =(H_sat-H_effectif)/2=(15-7)/2 = 4, c'est la bonne valeur.
Un autre exemple: le p.diaminobenzène
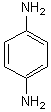Formule moléculaire C₆H₈N₂ dont le DI vaut 4 ( trois "liaisons p ", un cycle) :  H_sat= 14 +2 = 16    H_effectif=8 soit DI =(H_sat-H_effectif)/2=(16-8)/2 = 4

    3-4) Exemples à partir de composés halogénés:
Si l'on applique au chlorobenzène (C₆H₅Cl), la règle appliquée aux hydrocarbures ou aux composés oxygénés, on trouve: H_sat=14 et H_effectif=5 soit DI =(H_sat-H_effectif)/2=(14-5)/2 = 4,5 alors que la vraie valeur est 4.
Il faut donc pour les composés halogénés utiliser une autre règle pour le calcul de H_sat :

H_sat = 2n_C+2-n_X

La détermination du DI, avec H_sat calculé selon cette formule conduit bien à une valeur de 4:

H_sat=2x6+2-1=13    H_effectif=5 soit DI =(H_sat-H_effectif)/2=(13-5)/2 = 4.
    3-5) Règle générale de détermination du DI à partir de la formule moléculaire:

H_sat = 2n_C+2+n_N-n_X

puis

DI = (H_sat -H_effectif)/2 

Un exemple très général:
Détermination du degré d'insaturation d' une molécule de formule moléculaire C₂₂H₂₄O₈N₂
Hsat = 2x22 +2 +2 = 48
H_effectif= 24
DI = (Hsat -H_effectif)/2 = (48-24)/2 = 12
Ce qui peut être vérifié sur la formule de la tétracycline qui correspond à cette formule moléculaire:

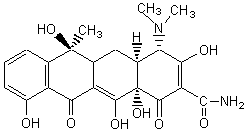
DI = 12 car on trouve 4 cycles et 8 liaisons p .

---

Autre exemple d'utilisation :
On souhaite établir la formule moléculaire d'une molécule assez complexe, par exemple l'acide chlorogénique :

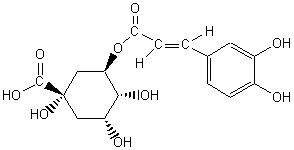
On compte les atomes de carbone et d'oxygène qui sont faciles à dénombrer : 16C et 9O. On utilise le degré d'insaturation qui est de 8 (6 doubles liaisons et 2 cycles) pour trouver le nombre d'H effectifs :
DI =(H_sat-H_effectif)/2
soit H_effectif = H_sat -2.DI = (2x16+2) - 2x8 = 18
La formule moléculaire de l'acide chlorogénique est C₁₆H₁₈O₉.

---